EXPL123 - Course Title Goes Here

Module x.x - Gay-Lussac's Gas Law

Throughout this module, you may use the on-screen arrows to navigate between sections. When you are ready to begin, click on the "begin" button below.

EXPL123 - Course Title Goes Here

Module x.x - Gay-Lussac's Gas Law

Module Progress:

Learning Objectives

Using Gay-Lussac's gas law, you should be able to describe the change that occurs in the initial versus the final temperature, and/or pressure of a gas, either through numeric calculations or statements of cause and effect. You must score 80% or higher on a formal assessment in order to successfully complete this module.

About This Module

Keep the following things in mind as we work through this module:

  • We will use Kelvin (marked as K) for our units of temperature. Using Kelvin is required for these calculations.
    • Converting Fahrenheit (°F) to Kelvin: Take the temperature in Fahrenheit and add 459.67 to it, then multiply that result by 5/9 (if not using a scientific calculator, you can first multiply by 5 and then divide by 9).
    • Converting Celcius (°C) to Kelvin: Just add 273.15 to the temperature in Celcius to get the equivalent temperature in Kelvin.
  • We will use Pounds per Square Inch (abbreviated as PSI) for units of pressure in our examples. Any units for pressure can be used, as long as they stay the same throughout the problem.
  • It might help to keep a calculator close by — any standard calculator will work.

Background

Woman Waving

Hey there! I'm Kayla, and I'll be your guide for this module. Together, we'll be looking at Gay-Lussac's Gas Law and how it affects our world on a daily basis. Don't believe me? Let's take a look at some examples.

Background

Woman Thinking

Have you ever noticed when opening a bottle of soda that's been in the fridge for a while, it barely lets out any "hiss"? In contrast, when you open one that's been sitting on the table, it lets out a large, very audible hissing sound.

Without opening the bottle, what factors might be different between when the bottle is in the fridge versus when it's outside the fridge? And beyond that, what determines the strength of the hissing sound when you open the bottle?

Background

Woman Thinking

How about a personal example? Last week, I used a tire pressure gauge to measure the air in my tires before a road trip. They all measured around 32psi before I left. After a while of driving, I used the gauge again to make sure my tires weren't losing any air, but to my surprise the gauge read 34psi!

I didn't stop to add any air, and tires definitely don't "suck in" air on their own. They're at a higher pressure than the outside air, so if anything, the air would want to escape. How could the pressure gauge read higher than when I left in the morning?

Background

Woman distressed with hands outstretched

It seems like all of these examples have something to do with a gas: The carbon dioxide in the soda and the air in the tires.

How do we know what's changing in each situation, though? It sounds like we need to set up an experiment and gather some data. I have just the friend who can help, too! Head to the next section when you're ready to meet him and observe the results.

Running Our Experiments: The Soda

Professor Parker Avatar Image

Hi! I'm Professor Parker, Kayla's friend, and I'll be running the experiments for us so we can observe the results. Click on the image below to start the experiment.

Running Our Experiments: Car Tires

Professor Parker Avatar Image

Now we're getting somewhere. We have two experiments with similar outcomes, but we'll still look at Kayla's road trip example for good measure. When you're ready, click to begin.

Analyzing the Results

Woman Smiling pointing one finger in air

There's definitely something going on with both the temperature and pressure of the gases in these experiments. Can you guess what it is?

Not quite — Our object is to figure out how the values are changing. Through our experiments, we were more focused on the patterns and the relationship between the values that are recorded rather than the fact that they are changing. Feel free to re-visit the experiments; pay attention to how the values change over the course of the experiment, and how those changes are mirrored across all three experiments. Once you feel like you've found a pattern, return here and select another option!
You nailed it! We can see in the experiments that when one of the factors changes, the other one also changes. What's more, an increase in one is also associated with an increase in the other, as the tests results showed.
Almost — there is a correlation between temperature and pressure, but we can see from the experiments that if the initial reading increases for one factor, the other one increases as well. Feel free to re-visit the experiments in the previous section and make another guess!
I like your outside-the-box thinking, but the volume actually stays constant during these examples. The soda bottle, the pipe, and the tire are all representative of containers which do not let any gas in, nor let any escape from inside. Therefore, we can say that the volume of the gas remained constant in our experiments. Feel free to re-visit the examples or select another option now that you have verified that the volume is constant!

Drawing a Conclusion

Woman with confident posture, arms crossed, smiling

You're well on your way to mastering Gay-Lussac's Law! You were correct in stating that temperature and pressure are correlated, and that as temperature increases, so does pressure (and vice versa).

In fact, Gay-Lussac's Law states that the changes in temperature and pressure are directly proportional, meaning that they both increase or decrease by the same amount. This means the formula for calculating the change can be written as:

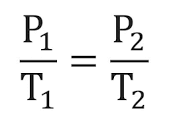
Gay-Lussac's Formula

where T1 is the starting temperature, T2 is the final temperature, P1 is the starting pressure, and P2 is the final pressure.

Keep in mind, though, that this law only works if the volume of the gas involved stays constant. Since the two environments we looked at kept the gas contained, the volume did not change and we could use this law.

How about we look at some new examples? When you're ready, press the "Continue" button to work through a couple more practice scenarios on your own.

Practice Exercises

Below are a few practice exercises for you to practice what you've seen so far in this module. You'll be presented with a couple example situations and must select the best answer to the question that's posed from a list of options.

Exercise 1

A student removes an airtight container of gas from a refrigerated storage at -10°F (249.81K) and places it on the table, allowing it to warm up to a room temperature of 68°F (293.15K). The pressure gauge on the container read 10PSI when he removed it from storage.

At room temperature, which is the most likely reading for the pressure gauge? (Hint: using the formula for Gay-Lussac's Law would give you the exact answer, but it is not required.)

Not quite - we know by following Gay-Lussac's Law that an increase in temperature would be correlated with an increase in pressure. Since we started at 10PSI from storage, the pressure would likely increase above 10PSI as the container warmed up.
A reading of 10PSI would mean that the pressure inside the container never changed while the temperature changed quite drastically. Gay-Lussac's Law states that, at a fixed volume, temperature and pressure are directly proportional to one another, so it would have to change in response to the change in temperature.
Nice Job! You could have used the formula to arrive at this answer, but you can also use Gay-Lussac's law to rule out the other 2 answers. Since we know pressure increases as temperature increases, we know that the first answer (a decrease in pressure) and second answer (no change in pressure) would be incorrect.

Practice Exercises

Exercise 2

An engineer is designing a pressure relief valve for a normally airtight gas container that should open if the pressure gets too high, in this case 200PSI. In its normal operating environment, the temperature of the room the gas container is located in measures about 300K, and the normal operating pressure inside the gas container is 100PSI.

Use Gay-Lussac's formula to calculate the temperature which the gas would need to reach before the safety system kicks in.

That's correct — Since Gay-Lussac's Law says that temperature and pressure are directly proportional, doubling the pressure from 100PSI to 200PSI would also double the temperature from 300K to 600K.
Hmm, let's dig a little deeper — Gay-Lussac's Law says that temperature and pressure are directly proportional, and in order for the safety valve to kick in, we need double the pressure when compared to normal operation. Gay-Lussac's Law also says that temperature and pressure are directly proportional, so when you do something to one, you have to do the same to the other (in this case, multiplying by 2). Do any of the other answers look like they might follow this pattern?
If the gas did not change in temperature at all but the pressure did, this would violate Gay-Lussac's Law. It may help to review the conclusions we arrived at after running our experiments.

Practice Exercises

Exercise 3

You put some food in a pressure cooker and close the lid. Before you start the cooking process, you press on the pressure relief valve on the top of the unit, and nothing happens. After several minutes of cooking, you press the valve again and hear a hissing sound, and determine this is the sound of pressure being released from inside the unit.

Which statement best uses Gay-Lussac's law to describe what happened?

Not quite — Remember that in Gay-Lussac's Law, the temperature and pressure move in the same direction, meaning that if one value increased, the other value would increase as well.
Correct! The increase in temperature produced an increase in pressure inside the pressure cooker while the food was cooking. Since the volume of air remained constant (until we pushed on the valve), Gay-Lussac's Law can be used to describe this correlation.
Almost! You are correct that, according to Gay-Lussac's law, the volume of the gas can't change. However, we don't measure the pressure after we press the valve down, but rather just use the hissing noise to confirm that the pressure did actually increase during the cooking process.